Курс:Спектральная теория систем ранга один
Материал из TDS
(Различия между версиями)
| (1 промежуточная версия не показана) | |||
| Строка 28: | Строка 28: | ||
---- | ---- | ||
[http://mech.math.msu.su/department/tds/wiki/images/e/e0/CourseElHouceinR1.pdf Программа курса в PDF] | [http://mech.math.msu.su/department/tds/wiki/images/e/e0/CourseElHouceinR1.pdf Программа курса в PDF] | ||
| + | |||
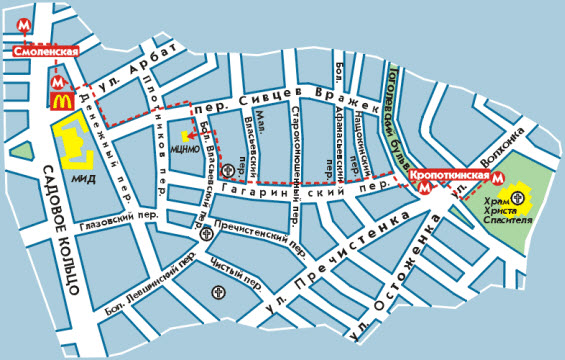
| + | [http://www.mccme.ru/head/address.html Как добраться?] | ||
| + | |||
| + | [[Image:Mccme.jpg]] | ||
---- | ---- | ||
''Курс читаться в МНУ МЦНМО. Первая лекция - 27 февраля 2012'' | ''Курс читаться в МНУ МЦНМО. Первая лекция - 27 февраля 2012'' | ||
Текущая версия на 15:39, 27 января 2012
Лектор - профессор El Houcein El Abdalaoui, Laboratoire de Mathématiques Raphaël Salem (LMRS), l'Université de Rouen
Курс читается на английском языке.
Организаторы: Кафедра теории динамических систем / МИАН / Русско-французская лаборатория Poncelet / МЦНМО
ПРОГРАММА КУРСА
Part I: Riesz products via harmonic analysis
In this part we discuss different classes of probability measures on R constructed with the help of Riesz products, including Salem question.
- a) Zygmund singularity criterion
- b) Theorem on mutual singularity due to Peyrière
Part II: Generalized Riesz products as spectral types of dynamical systems (Z-actions)
- Ledrappier example (classical Riesz products).
- Spectral type of the Morse substitution.
- On the spectral type of subsitutions with (multi-dimensional Riesz products) with applications to interval exchange transformations.
- Host-Parreau-Méla theorem.
- Spectral type of a rank one transformation via Bourgain technique.
- Bourgain singularity criterion.
- Conditions for existence of the Lebesgue component.
- Bourgain and Klemes-Reinhold theorems on spectral type of a rank one transformation.
Part III: Generalized Riesz products as spectral types of dynamical systemes (countable group actions)
- 9. Examples due to Ismagilov.
- 10. Helson-Parry and Guenais exemples.
Курс читаться в МНУ МЦНМО. Первая лекция - 27 февраля 2012