Спецкурс Методы визуализации:Задачи
Материал из TDS
| (16 промежуточных версий не показаны.) | |||
| Строка 1: | Строка 1: | ||
---- | ---- | ||
''ЗАДАЧИ СТАНДАРТНОЙ СЛОЖНОСТИ'' | ''ЗАДАЧИ СТАНДАРТНОЙ СЛОЖНОСТИ'' | ||
| + | |||
| + | ===Динамика сумм Вейля=== | ||
| + | |||
| + | [[Image:WeylSums1.png|390px]] | ||
| + | |||
| + | Задача: исследовать поведение экспоненциальных сумм с полиномиальной частотной функцией в зависимости от числа слагаемых. | ||
| + | |||
| + | ''Литература'' | ||
| + | * [http://arxiv.org/pdf/0909.3079v1.pdf A. Fedotov AND F. Klopp, An exact renormalization formula for Gaussian exponential sums and applications] | ||
| + | |||
| + | ===Фрактал Рози=== | ||
| + | |||
| + | [[Image:RauzyFractal.gif|240px]] | ||
| + | |||
| + | Задача: построить модель классического (двумерного) фрактала Рози, показывающую трансформацию фрактала под действием преобразований. | ||
| + | |||
| + | ===Множества Мандельброта и Жюлиа=== | ||
| + | |||
| + | <gallery> | ||
| + | Image: Mandelbr1.png | ||
| + | Image: Mandelbr1.png | ||
| + | Image: Mandelbr2.png | ||
| + | </gallery> | ||
| + | |||
| + | Задача: визуализировать процесс бесконечного приближения к некоторой точке границы множества Мандельброта на плоскости параметров, рисуя параллельно множество Жюлиа. | ||
===Тайлинги Пенроуза=== | ===Тайлинги Пенроуза=== | ||
| Строка 26: | Строка 51: | ||
* построить интерактивную модель "путешествия" по графу Кэли группы ''L''<sub>2</sub> (группа мигающих лампочек, lamplighter group), представленному в форме орициклического произведения деревьев | * построить интерактивную модель "путешествия" по графу Кэли группы ''L''<sub>2</sub> (группа мигающих лампочек, lamplighter group), представленному в форме орициклического произведения деревьев | ||
* нарисовать собственные функции оператора случайного блуждания | * нарисовать собственные функции оператора случайного блуждания | ||
| + | |||
| + | ===Предельные полиномы автоморфизма Чакона и голоморфная динамика=== | ||
| + | |||
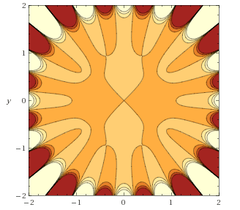
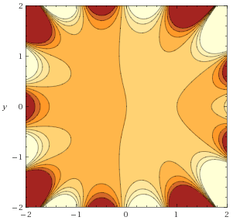
| + | [[Image:Phi_m1.png|240px]] [[Image:Phi_m05.png|240px]] | ||
| + | |||
| + | Задача: построить динамическую модель эволюции производящей функции семейства предельных полиномов в зависимости от параметра. | ||
| + | |||
| + | ''Литература'' | ||
| + | * [http://arxiv.org/abs/1207.0614 Aleksander Prikhod'ko, Valery Ryzhikov. Several questions and hypotheses concerning the limit polynomials for Chacon transformation] | ||
| + | * [http://arxiv.org/abs/math/0511397v1 Kathleen L. Petersen, Christopher D. Sinclair. Conjugate Reciprocal Polynomials with all Roots on the Unit Circle] | ||
===Геометрические свойства марковских полей и клеточных автоматов=== | ===Геометрические свойства марковских полей и клеточных автоматов=== | ||
| + | |||
| + | [[Image:h5.jpg|240px]] | ||
Задача: изобразить динамическую систему Ледрапье на плоскости '''Z'''<sup>2</sup> и исследовать полученное марковское поле | Задача: изобразить динамическую систему Ледрапье на плоскости '''Z'''<sup>2</sup> и исследовать полученное марковское поле | ||
| - | === | + | ===Клеточный автомат Life на торе=== |
| + | |||
| + | [[Image:Animated glider emblem.gif]] [[Image:LifeOnTorus.jpg|180px]] | ||
| + | |||
| + | Задача: визуализировать автомат "Life" Дж. Конвея на дискретном торе '''Z'''<sup>2</sup>/(''p'',''q'')'''Z'''<sup>2</sup>, где ''p'' и ''q'' - пара натуральных чисел. Исследовать динамику данного клеточного автомата в зависимости от параметров ''p'' и ''q''. | ||
| + | |||
| + | ===Изгибаемые многогранники=== | ||
| + | |||
| + | [[Image:StePoly.png]] | ||
| - | Задача: визуализировать пример | + | Задача: визуализировать пример ''изгибаемого'' (''нежёсткого'') многогранника (допускающего движение граней на стыке при сохранении геометрии граней). |
Текущая версия на 13:38, 23 ноября 2012
ЗАДАЧИ СТАНДАРТНОЙ СЛОЖНОСТИ
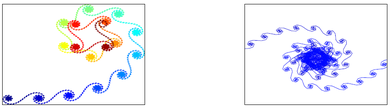
Динамика сумм Вейля
Задача: исследовать поведение экспоненциальных сумм с полиномиальной частотной функцией в зависимости от числа слагаемых.
Литература
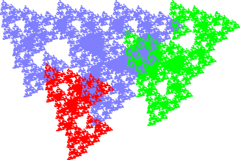
Фрактал Рози
Задача: построить модель классического (двумерного) фрактала Рози, показывающую трансформацию фрактала под действием преобразований.
Множества Мандельброта и Жюлиа
Задача: визуализировать процесс бесконечного приближения к некоторой точке границы множества Мандельброта на плоскости параметров, рисуя параллельно множество Жюлиа.
Тайлинги Пенроуза
Задача: изобразить тайлинги Пенроуза с дополнительными условиями раскраски фигур
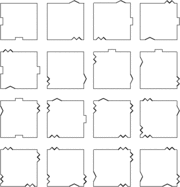
Тайлинги с определенными условиями на сочетания фигур
Задача:
- визуализировать замощения плоскости квадратами с заданными граничными условиями сочетания фигур
- исследовать сложность (энтропию) полученной динамической системы
Литература
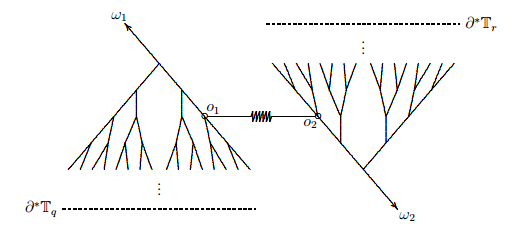
Группа Lamplighter
Задача:
- построить интерактивную модель "путешествия" по графу Кэли группы L2 (группа мигающих лампочек, lamplighter group), представленному в форме орициклического произведения деревьев
- нарисовать собственные функции оператора случайного блуждания
Предельные полиномы автоморфизма Чакона и голоморфная динамика
Задача: построить динамическую модель эволюции производящей функции семейства предельных полиномов в зависимости от параметра.
Литература
- Aleksander Prikhod'ko, Valery Ryzhikov. Several questions and hypotheses concerning the limit polynomials for Chacon transformation
- Kathleen L. Petersen, Christopher D. Sinclair. Conjugate Reciprocal Polynomials with all Roots on the Unit Circle
Геометрические свойства марковских полей и клеточных автоматов
Задача: изобразить динамическую систему Ледрапье на плоскости Z2 и исследовать полученное марковское поле
Клеточный автомат Life на торе
Задача: визуализировать автомат "Life" Дж. Конвея на дискретном торе Z2/(p,q)Z2, где p и q - пара натуральных чисел. Исследовать динамику данного клеточного автомата в зависимости от параметров p и q.
Изгибаемые многогранники
Задача: визуализировать пример изгибаемого (нежёсткого) многогранника (допускающего движение граней на стыке при сохранении геометрии граней).
БОЛЕЕ СЛОЖНЫЕ ЗАДАЧИ
Визуализация трёхмерного фрактала Рози
(***)