Спецкурс Методы визуализации

Материал из TDS

Версия 18:33, 7 октября 2012 (просмотреть исходный код) Александр Приходько (обсуждение | вклад) ← Предыдущая правка		Версия 10:32, 8 октября 2012 (просмотреть исходный код) Александр Приходько (обсуждение | вклад) Следующая правка →
Строка 34:		Строка 34:
-	==Экзаменационные задания==	+	{{:Спецкурс Методы визуализации:Задачи}}
-		+
-	Слушатели могут выбрать задание из списка или предложить собственную задачу, связанную с темой научной работы.	+
-		+
-	----	+
-	''ЗАДАЧИ СТАНДАРТНОЙ СЛОЖНОСТИ''	+
-		+
-	===Тайлинги Пенроуза===	+
-		+
-	Задача: изобразить тайлинги Пенроуза с дополнительными условиями раскраски фигур	+
-		+
-	===Тайлинги с определенными условиями на сочетания фигур===	+
-		+
-	Задача:	+
-	* визуализировать замощения плоскости квадратами с заданными граничными условиями сочетания фигур	+
-	* исследовать сложность (энтропию) полученной динамической системы	+
-		+
-	===Группа Lamplighter===	+
-		+
-	Задача:	+
-	* построить интерактивную модель "путешествия" по графу Кэли группы ''L''<sub>2</sub> (группа мигающих лампочек, lamplighter group), представленному в форме орициклического произведения деревьев	+
-	* нарисовать собственные функции оператора случайного блуждания	+
-		+
-	===Геометрические свойства марковских полей и клеточных автоматов===	+
-		+
-	Задача: изобразить динамическую систему Ледрапье на плоскости '''Z'''<sup>2</sup> и исследовать полученное марковское поле	+
-		+
-	===Нежесткие многогранники===	+
-		+
-	Задача: визуализировать пример нежесткого многогранника (допускающего движение граней на стыке при сохранении геометрии граней)	+
-		+
-		+
-	----	+
-	''БОЛЕЕ СЛОЖНЫЕ ЗАДАЧИ''	+
-		+
-	===Визуализация трёхмерного фрактала Рози===	+
-	(***)	+

---

Версия 10:32, 8 октября 2012

Введение в методы динамической визуализации с приложениями к теории дифференциальных уравнений

Лекторы: к.ф.-м.н. А.А. Приходько, к.ф.-м.н. И.В. Щуров

Содержание 1 Анонс спецкурса 2 Учебные материалы 2.1 "Рабочие тетради" 2.2 Динамика сумм Вейля 2.3 Фрактал Рози 2.4 Множества Мандельброта и Жюлиа 2.5 Тайлинги Пенроуза 2.6 Тайлинги с определенными условиями на сочетания фигур 2.7 Группа Lamplighter 2.8 Предельные полиномы автоморфизма Чакона и голоморфная динамика 2.9 Геометрические свойства марковских полей и клеточных автоматов 2.10 Клеточный автомат Life на торе 2.11 Изгибаемые многогранники 2.12 Визуализация трёхмерного фрактала Рози

Анонс спецкурса

В нашем спецкурсе мы изучим несколько простейших приемов визуализации динамических систем, фазовых портретов дифференциальных уравнений, самоподобных и фрактальных структур, а также некоторых конструкций дискретной геометрии. Мы познакомимся с несколькими компьютерными технологиями визуализации, а также разберём соответствующие математические модели.

Спецкурс ориентирован на студентов 1 - 3 курсов. Загрузить постер...

Фракталы	Тайлинги Пенроуза	Системы классической механики
Топологическая динамика	Символическая динамика. Графы. Комбинаторная теория групп	Аттракторы. Эргодические свойства динамических систем

Лекции будут проходить по субботам с 15:00 в ауд. 12-07 (ГЗ).

Первая лекция - 22 сентября.

Слушателей просим записаться, отправив сообщение на адрес: sasha.prihodko@gmail.com

Учебные материалы

"Рабочие тетради"

• Лекция 1
• Лекция 2

(рекомендуется при загрузке выбирать команду: правая кнопка мыши, Загрузить объект как...)

---

ЗАДАЧИ СТАНДАРТНОЙ СЛОЖНОСТИ

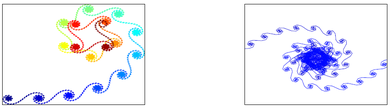
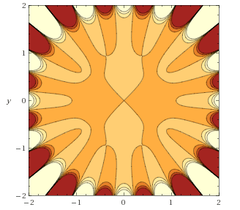
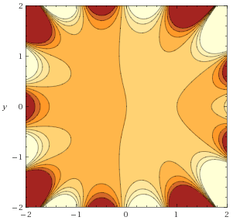
Динамика сумм Вейля

Задача: исследовать поведение экспоненциальных сумм с полиномиальной частотной функцией в зависимости от числа слагаемых.

Литература

• A. Fedotov AND F. Klopp, An exact renormalization formula for Gaussian exponential sums and applications

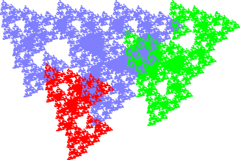
Фрактал Рози

Задача: построить модель классического (двумерного) фрактала Рози, показывающую трансформацию фрактала под действием преобразований.

Множества Мандельброта и Жюлиа

Задача: визуализировать процесс бесконечного приближения к некоторой точке границы множества Мандельброта на плоскости параметров, рисуя параллельно множество Жюлиа.

Тайлинги Пенроуза

Задача: изобразить тайлинги Пенроуза с дополнительными условиями раскраски фигур

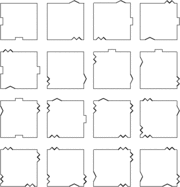
Тайлинги с определенными условиями на сочетания фигур

Задача:

• визуализировать замощения плоскости квадратами с заданными граничными условиями сочетания фигур
• исследовать сложность (энтропию) полученной динамической системы

Литература

• Quasicrystals: Solids with Unusual Symmetry

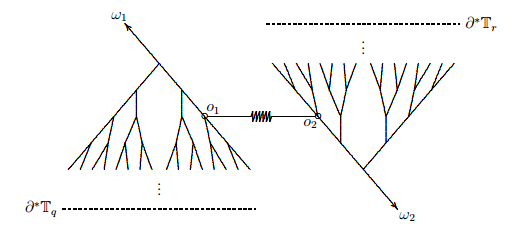
Группа Lamplighter

Задача:

• построить интерактивную модель "путешествия" по графу Кэли группы L₂ (группа мигающих лампочек, lamplighter group), представленному в форме орициклического произведения деревьев
• нарисовать собственные функции оператора случайного блуждания

Предельные полиномы автоморфизма Чакона и голоморфная динамика

Задача: построить динамическую модель эволюции производящей функции семейства предельных полиномов в зависимости от параметра.

Литература

• Aleksander Prikhod'ko, Valery Ryzhikov. Several questions and hypotheses concerning the limit polynomials for Chacon transformation
• Kathleen L. Petersen, Christopher D. Sinclair. Conjugate Reciprocal Polynomials with all Roots on the Unit Circle

Геометрические свойства марковских полей и клеточных автоматов

Задача: изобразить динамическую систему Ледрапье на плоскости Z² и исследовать полученное марковское поле

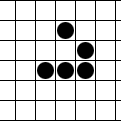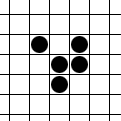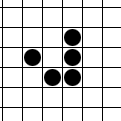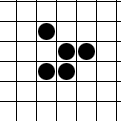
Клеточный автомат Life на торе

Задача: визуализировать автомат "Life" Дж. Конвея на дискретном торе Z²/(p,q)Z², где p и q - пара натуральных чисел. Исследовать динамику данного клеточного автомата в зависимости от параметров p и q.

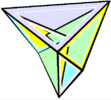
Изгибаемые многогранники

Задача: визуализировать пример изгибаемого (нежёсткого) многогранника (допускающего движение граней на стыке при сохранении геометрии граней).

---

БОЛЕЕ СЛОЖНЫЕ ЗАДАЧИ

Визуализация трёхмерного фрактала Рози

(***)