Спецкурс Методы визуализации:Задачи
Материал из TDS
(Различия между версиями)
| Строка 35: | Строка 35: | ||
===Клеточный автомат Life на торе=== | ===Клеточный автомат Life на торе=== | ||
| - | [[Image:Animated glider emblem.gif]] [[Image:LifeOnTorus.jpg| | + | [[Image:Animated glider emblem.gif]] [[Image:LifeOnTorus.jpg|180px]] |
Задача: визуализировать автомат "Life" Дж. Конвея на дискретном торе '''Z'''<sup>2</sup>/(''p'',''q'')'''Z'''<sup>2</sup>, где ''p'' и ''q'' - пара натуральных чисел. Исследовать динамику данного клеточного автомата в зависимости от параметров ''p'' и ''q''. | Задача: визуализировать автомат "Life" Дж. Конвея на дискретном торе '''Z'''<sup>2</sup>/(''p'',''q'')'''Z'''<sup>2</sup>, где ''p'' и ''q'' - пара натуральных чисел. Исследовать динамику данного клеточного автомата в зависимости от параметров ''p'' и ''q''. | ||
Версия 11:19, 8 октября 2012
ЗАДАЧИ СТАНДАРТНОЙ СЛОЖНОСТИ
Содержание |
Тайлинги Пенроуза
Задача: изобразить тайлинги Пенроуза с дополнительными условиями раскраски фигур
Тайлинги с определенными условиями на сочетания фигур
Задача:
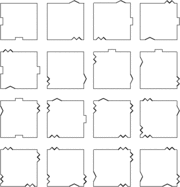
- визуализировать замощения плоскости квадратами с заданными граничными условиями сочетания фигур
- исследовать сложность (энтропию) полученной динамической системы
Литература
Группа Lamplighter
Задача:
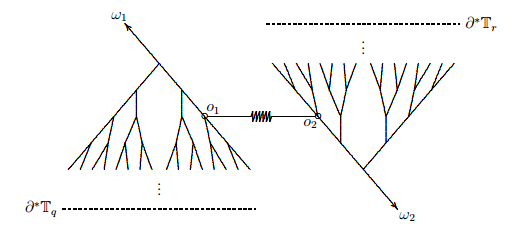
- построить интерактивную модель "путешествия" по графу Кэли группы L2 (группа мигающих лампочек, lamplighter group), представленному в форме орициклического произведения деревьев
- нарисовать собственные функции оператора случайного блуждания
Геометрические свойства марковских полей и клеточных автоматов
Задача: изобразить динамическую систему Ледрапье на плоскости Z2 и исследовать полученное марковское поле
Клеточный автомат Life на торе
Задача: визуализировать автомат "Life" Дж. Конвея на дискретном торе Z2/(p,q)Z2, где p и q - пара натуральных чисел. Исследовать динамику данного клеточного автомата в зависимости от параметров p и q.
Изгибаемые многогранники
Задача: визуализировать пример изгибаемого (нежёсткого) многогранника (допускающего движение граней на стыке при сохранении геометрии граней).
БОЛЕЕ СЛОЖНЫЕ ЗАДАЧИ
Визуализация трёхмерного фрактала Рози
(***)