ФИВТ:ДС:Лабораторные работы

Материал из TDS

Версия 16:11, 23 ноября 2012

Солитоны в проливе Гибралтар

© NASA, фотоснимок STS-41-G (Challenger), источник: http://www.lpi.usra.edu/

Исследовательские задачи

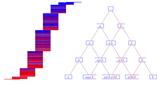
1. Исследовать динамику оператора диффузии на графе Spider Web Network. Вычислить и изучить асимптотическое поведение собственных функций этого оператора.
   • Описание модели: Ajit C. Balram, Deepak Dhar. Non-perturbative corrections to mean-field behavior: spherical model on spider-web graph
   • Дополнительная литература:
2. Построить модель клеточного автомата на графе Кэли дискретной неабелевой группе. В качестве основного случая можно рассмотреть группы BS(1,2) и H₃ и клеточный автомат Life. Получить экспериментальную оценку энтропии клеточного автомата, возникающего на конечном однородном пространстве группы (H₃, Z²).
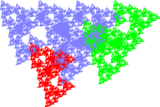
3. Визуализировать трехмерный фрактал Рози.
   • О классическом фрактале Рози
     • Web-Обзор Fractal de Rauzy
     • A. Siegel. Spectral theory for dynamical systems arising from substitutions (PDF)
     • V. Berthe, A. Siegel, J. Thuswaldner. Substitutions, Rauzy fractals, and tilings
     • Anne Siegel, Jorg M. Thuswaldner. Topological properties of Rauzy fractals
   • Дальнейшее развитие теории
     • N. Pytheas Fogg. Substitutions in Dynamics, Arithmetics and Combinatorics. (edt. by V. Berthe, S. Ferenczi, C. Mauduit, A. Siegel.) Глава 7 (описание системы)
     • Nicolas Bédaride, Jean françois Bertazzon. Minoration of the complexity function associated to a translation on the torus (одна из моделей)
     • Fabien Durand, Ali Messaoudi. Boundary of the Rauzy fractal set in R x C generated by P(x) = x⁴-x³-x²-x-1
4. Экспериментальное исследование динамических систем с применением распределенных вычислений:
   • а) оценка сумм Вейля
     Литература:
     • A. Fedotov AND F. Klopp, An exact renormalization formula for Gaussian exponential sums and applications
   • б) перемешивающие свойства автоморфизма Паскаля
     Литература:
     • Xavier Mela, Karl Petersen. Dynamical properties of the Pascal adic transformation
   • в) поиск конструктивных примеров плоских полиномов Литлвуда, соответствующих квантовым солитонам с мультипликативной симметрией спектра
     Литература:
     • Александр Приходько. О семействах плоских полиномов Литлвуда с унимодулярными коэффициентами

Визуализация динамических систем

Дополнительный список задач можно найти на странице курса Методы визуализации динамических систем (раздел Экзаменационные задания)

Работы будут включены в Библиотеку визуальных моделей динамических систем.