Курс:Потоки на однородных пространствах и распределение последовательностей Кронекера

Материал из TDS

Лектор - профессор Bassam Fayad, Institut de Mathématiques de Jussieu

Курс читается на английском языке.

Организаторы: Кафедра теории динамических систем / МИАН / Русско-французская лаборатория Poncelet / МЦНМО

Аннотация курса

Мы изучаем последовательности Кронекера n α на торе T^d, предполагая, что параметр α равномерно распределён на T^d. В одномерном случае, Кестен доказал (1960-е), что отклонение от главного члена асимптотики числа посещений последовательностью Кронекера случайного интервала, делённое на ln N, сходится к распределению Коши.

Существует два естественных способа обобщить эту проблему в многомерном случае: в качестве области в T^d мы можем рассмотреть как шар, так и куб. Поведение исследуемой последовательности связано с так называемыми малыми знаменателями, и сложность задачи, в частности, объясняется тем, что не все результаты теории (одномерных) непрерывных дробей перенесены на многомерный случай.

Используя эргодическую теорию потоков на однородных пространствах, мы покажем, что отклонение в асимптотике посещения шара, нормализованное коэффициентом N^(d-1)/2d, сходится к некоторому "нестандартному" распределению, а нормализованное отклонение в асимптотике для кубов с коэффициентом (ln N)</sup>-d</sup> сходится к распределению Коши.

Ключевым ингредиентом докуазательства является теорема Пуассона, примененённая к действию Картана на пространстве d+1-мерных решёток.

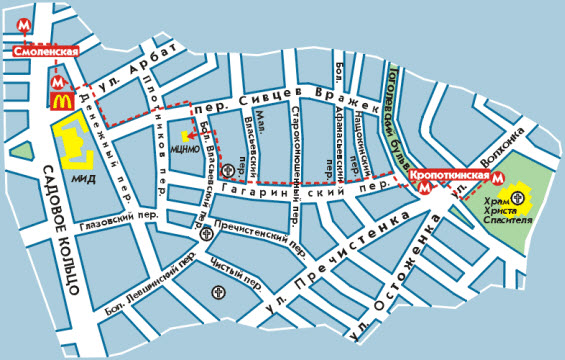
Курс будет читаться в МЦНМО:

• лекция 1-2: в среду 03.10, 17:30 - 21:00 ауд.303,
• лекция 3-4: в среду 10.10, 17:30 - 21:00 ауд.303

Программа курса в PDF

Как добраться?

Курс читаться в МНУ (МЦНМО). Первая лекция - 3 октября 2012