Спецкурсы 2012/13
Материал из TDS
| Строка 31: | Строка 31: | ||
==Спецкурсы== | ==Спецкурсы== | ||
| + | |||
| + | ===Спецкурс=== | ||
| + | |||
| + | '''Введение в аддитивную комбинаторику''' | ||
| + | |||
| + | Проф. [[Шкредов Илья Дмитриевич|И.Д. Шкредов]] | ||
| + | |||
| + | ''ПРОГРАММА КУРСА'' | ||
| + | * Введение. Простейшие соотношения между размерами сумм множеств. Неравенство Плюннеке. Универсальные множества. | ||
| + | * Анализ Фурье на абелевых группах. Равномерные множества первого порядка. Теорема Рота. | ||
| + | * Структура множеств с малым удвоением. Леммы о покрытиях. Теорема Фреймана в группах с кручением. | ||
| + | * Теорема Балога-Семереди-Гауэрса. Нормы Гауэрса, равномерные множества старших порядков. | ||
| + | * Свойства множеств Бора. | ||
| + | * Большие тригонометрические суммы. Теорема Фреймана, общая схема доказательства. | ||
| + | * Почти периодичность сверток характеристических функций. Арифметические прогрессии в суммах множеств. | ||
| + | * Теорема Фреймана, полиномиальная гипотеза Боголюбова --- современные оценки. | ||
| + | * Конструкция Беренда множеств без решений аффинных уравнений. Верхние оценки. | ||
| + | * Теорема Семереди-Трёттер, выпуклые множества. Суммы произведений: вещественный случай. | ||
| + | * Суммы произведений: конечные поля, равномерная распределенность мультипликативных подгрупп. | ||
| + | * Проблема Какея. | ||
| + | |||
| + | Спецкурс будет проходить в [http://ium.mccme.ru/ Независимом университете] по понедельникам в 17:30, ауд. 303. | ||
| + | |||
| + | Первое занятие --- 24-го сентября. | ||
===Спецкурс=== | ===Спецкурс=== | ||
| Строка 36: | Строка 60: | ||
'''Эргодическая теория и некоторые задачи классического анализа''' | '''Эргодическая теория и некоторые задачи классического анализа''' | ||
| - | [[Приходько Александр Александрович|А.А. Приходько]] | + | К.ф.-м.н. [[Приходько Александр Александрович|А.А. Приходько]] |
Спецкурс ориентирован на студентов 1 - 3 курсов. Первая часть курса | Спецкурс ориентирован на студентов 1 - 3 курсов. Первая часть курса | ||
Версия 11:12, 17 сентября 2012
Содержание |
Спецсеминары
Кафедральный спецсеминар
Динамические системы и их приложения
Семинар будет посвящён обсуждению и решению различных задач теории динамических систем, теории чисел, функционального анализа и математической физики.
Основные темы осеннего семестра:
- алгебраические и геометрические свойства динамических систем,
- аддитивная комбинаторика,
- диофантовы аппроксимации,
- эргодический подход к геометрии групп,
- символическая динамика, адические системы и сложность динамических систем,
- некоторые задачи теории аппроксимации действий с инвариантной мерой,
- солитоны и их связь со спектральной теорией динамических систем.
Уровень: для студентов 1 - 4 курсов
Семинар проходит по четвергам с 18:30 в ауд. 447 (2-й ГУМ).
Первое заседание: 27 сентября.
Исследовательский семинар
Динамические системы и эргодическая теория
Семинар проходит по понедельникам с 18:30 в ауд. 13-11 (ГЗ).
Первое заседание: 17 сентября.
Спецкурсы
Спецкурс
Введение в аддитивную комбинаторику
Проф. И.Д. Шкредов
ПРОГРАММА КУРСА
- Введение. Простейшие соотношения между размерами сумм множеств. Неравенство Плюннеке. Универсальные множества.
- Анализ Фурье на абелевых группах. Равномерные множества первого порядка. Теорема Рота.
- Структура множеств с малым удвоением. Леммы о покрытиях. Теорема Фреймана в группах с кручением.
- Теорема Балога-Семереди-Гауэрса. Нормы Гауэрса, равномерные множества старших порядков.
- Свойства множеств Бора.
- Большие тригонометрические суммы. Теорема Фреймана, общая схема доказательства.
- Почти периодичность сверток характеристических функций. Арифметические прогрессии в суммах множеств.
- Теорема Фреймана, полиномиальная гипотеза Боголюбова --- современные оценки.
- Конструкция Беренда множеств без решений аффинных уравнений. Верхние оценки.
- Теорема Семереди-Трёттер, выпуклые множества. Суммы произведений: вещественный случай.
- Суммы произведений: конечные поля, равномерная распределенность мультипликативных подгрупп.
- Проблема Какея.
Спецкурс будет проходить в Независимом университете по понедельникам в 17:30, ауд. 303.
Первое занятие --- 24-го сентября.
Спецкурс
Эргодическая теория и некоторые задачи классического анализа
К.ф.-м.н. А.А. Приходько
Спецкурс ориентирован на студентов 1 - 3 курсов. Первая часть курса представляет собой элементарное введение в динамические системы и эргодическую теорию. Мы рассмотрим следующие темы: примеры и основные конструкции динамчиеских систем, эргодическая теорема, динамическая энтропия и сложность, спектральные инварианты. Вторая часть курса посвящена задачам исследования свойств сингулярных вероятностных распределений, восходящим к работам Зигмунда, Харди и Литлвуда, и обсуждению взаимосвязи этого круга задач с конструкциями спектральной теории.
Лекции будут проходить по четвергам с 16:45 в ауд. 447 (2-й ГУМ).
Первая лекция - 20 сентября 2012 г.
Спецкурс-практикум
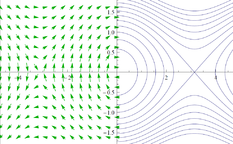
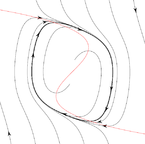
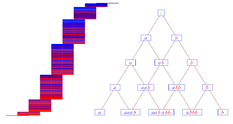
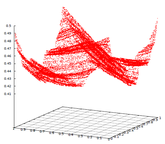
Введение в методы динамической визуализации с приложениями к теории дифференциальных уравнений
Лекторы: А.А. Приходько, И.В. Щуров
В нашем спецкурсе мы изучим несколько простейших приемов визуализации динамических систем, фазовых портретов дифференциальных уравнений, самоподобных и фрактальных структур, а также некоторых конструкций дискретной геометрии. Мы познакомимся с несколькими компьютерными технологиями визуализации, а также разберем соответствующие математические модели.
Спецкурс ориентирован на студентов 1 - 3 курсов.
Лекции будут проходить по субботам с 15:00 в ауд. 12-07 (ГЗ).
Первая лекция - 22 сентября.
Слушателей просим записаться, отправив сообщение на адрес: sasha.prihodko@gmail.com